Distributed Enterprise Systems (CO3409) Lab 18: Petri Nets

You can work on this problem by pen and paper, or using PIPE, or both.

18.1 Petri net analysis

Consider the Petri net below (see also the XML input file for PIPE):

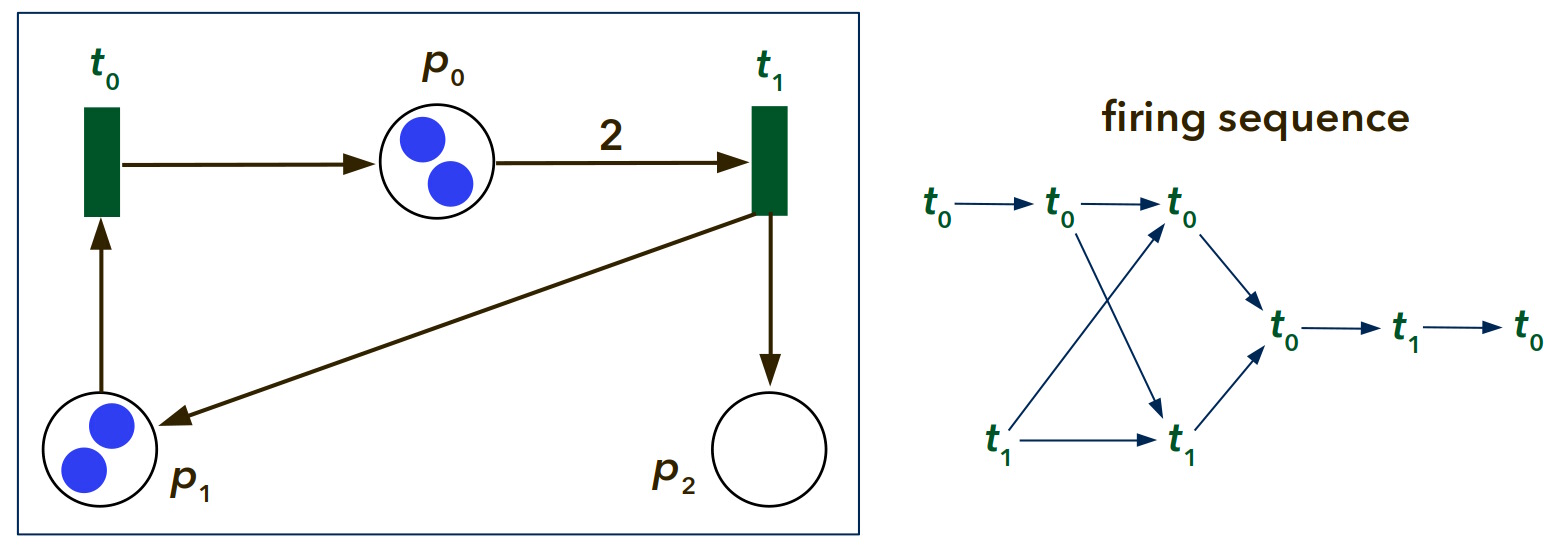
Make sure that you understand why the net exhibits the following behaviour:

1. Transitions can be fired in the following order: t₀t₀t₁t₀t₁t₀t₁t₀, t₀t₀t₁t₁t₀t₀t₁t₀, t₀t₁t₀t₀t₁t₀t₁t₀, t₀t₁t₀t₁t₀t₀t₁t₀, t₁t₀t₀t₀t₁t₀t₁t₀, and t₁t₀t₀t₁t₀t₀t₁t₀. At that point, respectively, a deadlock is reached.
2. The net is not safe: Places can contain more than one token.
3. Firing any of the transitions preserves the overall number of tokens (hence, the total number of tokens constitutes an invariant - it does not change).
4. The net is bounded: There is a limit (greater than one, but finite) to the number of tokens in every place.

The screenshots below illustrate the analysis functionality from PIPE. However, pen and paper should be enough to establish the observations made above.

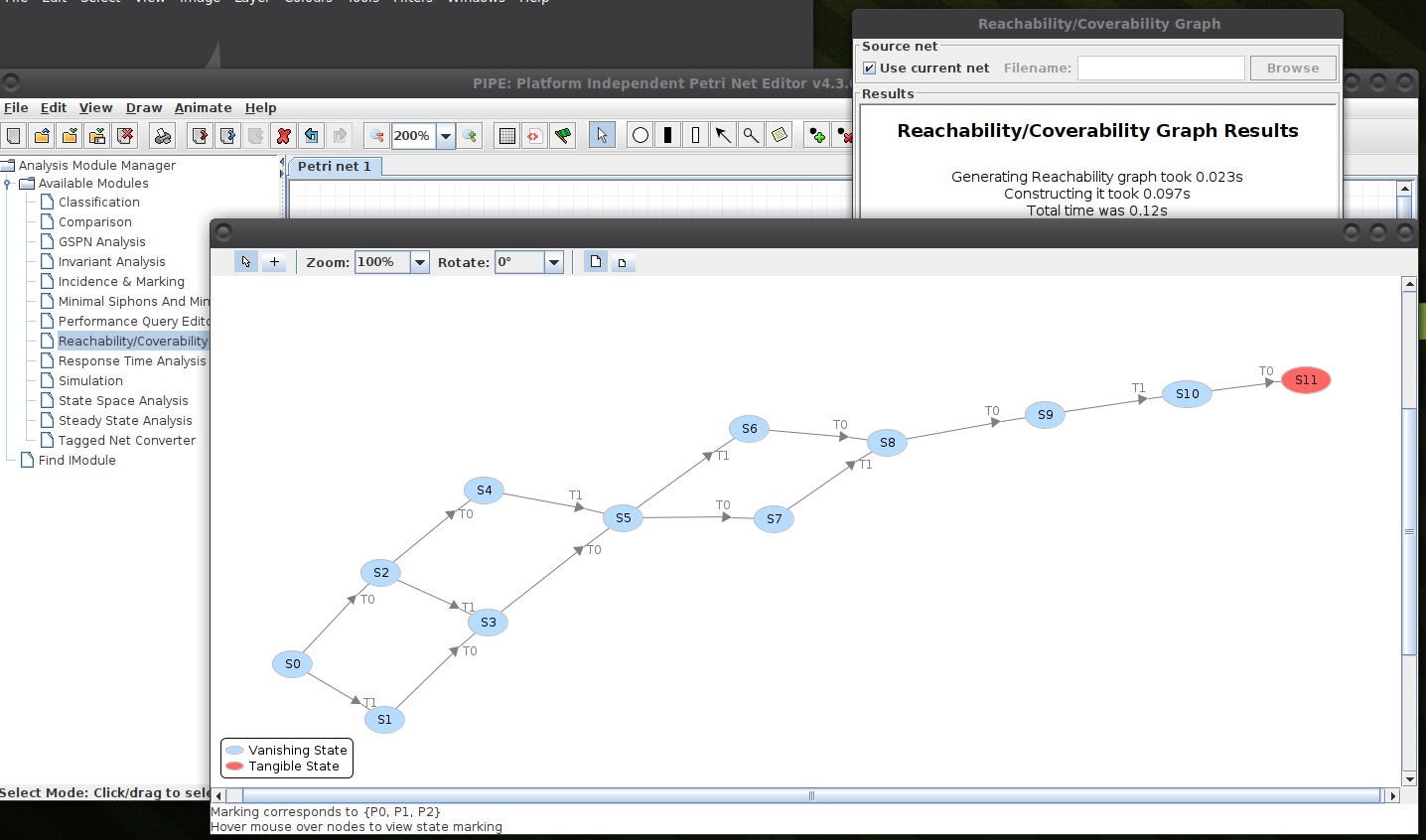
18.2 Petri net design

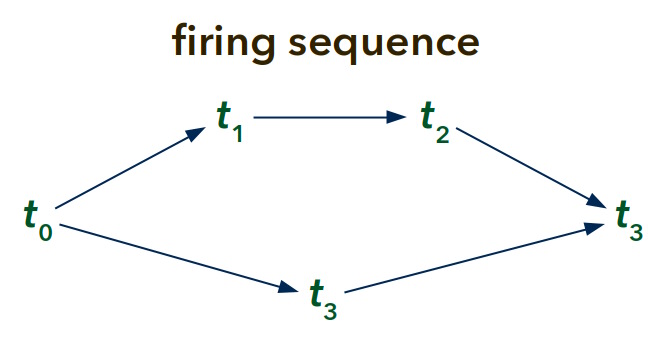
1. Design a Petri net with four transitions that can (only) be fired as follows until a deadlock is reached: t₀t₁t₂t₃t₃, t₀t₁t₃t₂t₃, and t₀t₃t₁t₂t₃.
2. Is your net safe? Is it bounded?

If you are interested in feedback on your work, send an email to Aaron Bryant and Martin Horsch.